Algoritmo BFS. 

Antes de empezar con la implementación te explicamos a grandes rasgos que es el algoritmo BFS.

BFS

El algoritmo BFS (Breadth-First Search o Búsqueda en Amplitud) es otro algoritmo de búsqueda utilizado en grafos. A diferencia de DFS, que explora tan lejos como sea posible a lo largo de cada rama antes de retroceder, BFS explora los nodos vecinos del nodo actual antes de pasar a los nodos que están más lejos. 

La idea clave detrás de BFS es que explora todos los nodos a la misma profundidad antes de pasar a los nodos en la siguiente profundidad. Esto garantiza que se encuentren los nodos más cercanos al nodo raíz antes de explorar nodos más lejanos.

BFS es útil para encontrar el camino más corto entre dos nodos en un grafo no ponderado, ya que garantiza que el primer camino que se encuentre entre los nodos raíz y objetivo será el más corto en términos de número de aristas. También se utiliza en la resolución de problemas de búsqueda en grafos, como la búsqueda en redes sociales o la resolución de problemas de ruteo en redes de computadoras.

Aplicaciones del BFS.

• Búsqueda de caminos más cortos: BFS se utiliza para encontrar el camino más corto entre dos nodos en un grafo no ponderado. Es útil en aplicaciones como la navegación GPS para encontrar la ruta más rápida entre dos ubicaciones.
• Grafos de redes sociales: En redes sociales como Facebook o Twitter, BFS se utiliza para encontrar amigos o conexiones entre usuarios. Por ejemplo, puede ayudar a encontrar amigos de amigos dentro de una red social.
• Resolución de laberintos: BFS se puede utilizar para encontrar la solución más corta a un laberinto. Cada celda del laberinto se representa como un nodo, y BFS se usa para encontrar la ruta desde la entrada hasta la salida del laberinto.
• Verificación de conectividad: BFS se utiliza para verificar la conectividad entre nodos en una red o grafo. Puede ayudar a determinar si todos los nodos en una red están interconectados o si hay nodos aislados.
• Búsqueda de componentes conectados: BFS se utiliza para encontrar componentes conectados en un grafo. Puede ayudar a identificar grupos de nodos que están conectados entre sí pero no están conectados a otros grupos de nodos.

Si deseas profundizar mas en el tema puedes ingresar a nuestro blog donde detallamos de mejor manera este tema  https://asimov.cloud/blog/programacion-5/algoritmos-dfs-y-bfs-en-un-grafo-199 

Implementación en Python. 

Imagina que deseas recorrer por BFS el siguiente grafo.

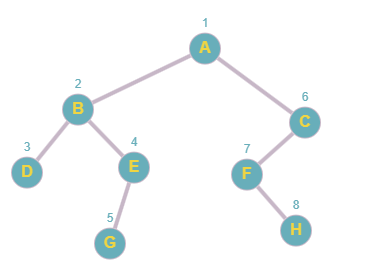
El procedimiento seria el siguiente:

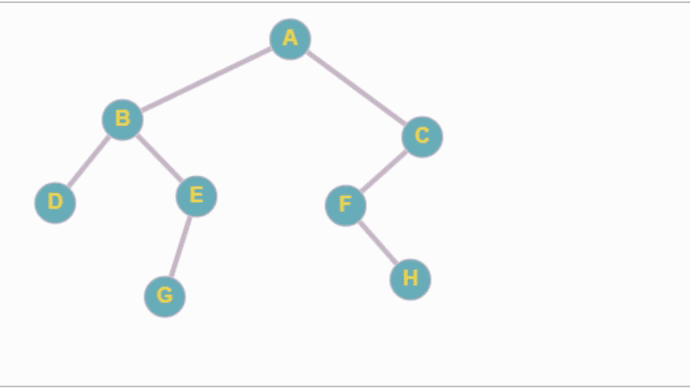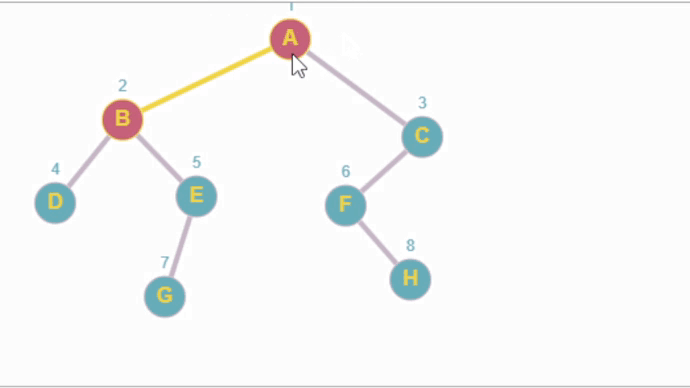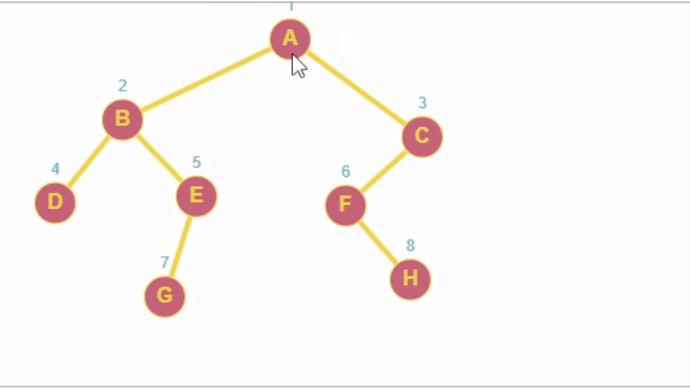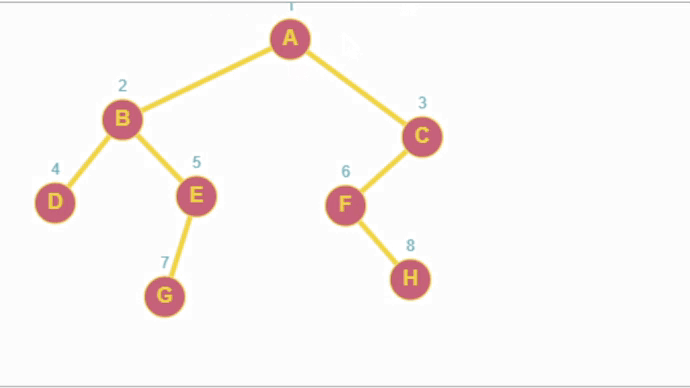
La codificación en Python seria la siguiente:

Si quiere aprender a detalle como programar un grafo en Python le recomendamos nuestro blog: https://asimov.cloud/blog/programacion-5/programar-un-grafo-en-python-263#scrollTop=0 , donde explicamos como implementar un grafo en Python:

from collections import deque

class Graph:

    def __init__(self):
        # Constructor de la clase Graph. Inicializa un diccionario para representar el grafo.
        self.graph = {}

    def add_vertex(self, vertex):
        # Método para agregar un vértice al grafo.
        if vertex not in self.graph:
            # Si el vértice no está en el grafo, lo agrega con un diccionario vacío para representar sus conexiones.
            self.graph[vertex] = {}

    def add_edge(self, vertex1, vertex2, weight=None, directed=False):
        # Método para agregar una arista al grafo entre dos vértices dados.
        self.add_vertex(vertex1)  # Aseguramos que los vértices estén presentes en el grafo.
        self.add_vertex(vertex2)

        self.graph[vertex1][vertex2] = weight  # Añade una conexión desde vertex1 a vertex2 con el peso dado.

        if not directed:
            # Si el grafo no es dirigido, añade también una conexión desde vertex2 a vertex1 con el mismo peso.
            self.graph[vertex2][vertex1] = weight

    def display(self):

        # Método para mostrar el grafo en forma legible.
        for vertex, edges in self.graph.items():

            print(f"Vértice {vertex} tiene como conexiones a:")
            for neighbor, weight in edges.items():

                if weight:
                    # Si hay peso en la conexión, imprime el vecino y su peso.
                    print(f"  - {neighbor} (peso: {weight})")

                else:
                    # Si no hay peso, imprime solo el vecino.
                    print(f"  - {neighbor}")


    def bfs_traversal(self, start_vertex):

        # Método para realizar un recorrido en anchura (Breadth-First Search) desde un vértice dado.
        visited = set()  # Conjunto para almacenar los vértices visitados
        queue = deque([start_vertex])  # Cola para almacenar los vértices que se van a visitar

        while queue:

            vertex = queue.popleft()  # Sacamos un vértice de la cola

            if vertex not in visited:
                print(vertex, end=" ")  # Imprimimos el vértice actual
                visited.add(vertex)  # Marcamos el vértice como visitado

                # Agregamos los vecinos del vértice actual a la cola
                for neighbor in self.graph[vertex]:

                    if neighbor not in visited:
                        queue.append(neighbor)


# Ejemplo de uso:

g = Graph()

g.add_edge('A', 'B', weight=1)
g.add_edge('A', 'C', weight=1)
g.add_edge('B', 'D', weight=1)
g.add_edge('B', 'E', weight=1)
g.add_edge('C', 'F', weight=1)
g.add_edge('E', 'G', weight=1)
g.add_edge('F', 'H', weight=1)

print("Recorrido BFS:")
g.bfs_traversal('A')

Resultados.

Al ejecutar el programa el resultado obtenido es el siguiente: 

             Recorrido BFS:            
            A B C D E F G H