¿Qué es el algoritmo Dijkstra ?
A grandes rasgos el algoritmo de Dijkstra encuentra el camino más corto desde un nodo de inicio hacia todos los demás nodos en un grafo, donde cada arista tiene un peso no negativo. Comienza desde el nodo de inicio, expandiéndose gradualmente hacia otros nodos mediante la selección de la ruta más corta disponible en cada paso. Finalmente, determina las distancias mínimas a todos los nodos.
Programación en Python.
Antes de implementar el algoritmo debemos tener una clase grafo, dicho código se muestra a continuación.
#Codigo Grafo
class Graph: def __init__(self): self.graph = {} def add_vertex(self, vertex): if vertex not in self.graph: self.graph[vertex] = {} def add_edge(self, vertex1, vertex2, weight=None, directed=False): if vertex1 not in self.graph: self.add_vertex(vertex1) if vertex2 not in self.graph: self.add_vertex(vertex2) self.graph[vertex1][vertex2] = weight if not directed: self.graph[vertex2][vertex1] = weight
Después basta se agrega un nuevo método a la clase llamado "dijkstra", dicho método es el siguiente:
def dijkstra(self, start):
distances = {vertex: float('infinity') for vertex in self.graph}
distances[start] = 0
queue = [(0, start)]
while queue:
current_distance, current_vertex = heapq.heappop(queue)
if current_distance > distances[current_vertex]:
continue
for neighbor, weight in self.graph[current_vertex].items():
distance = current_distance + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor))
return distances
Si bien el algoritmo funciona, y es posible implementarlo sin profundizar en detalle a continuación te mostramos la explicación :
Primero definimos un método "dijkstra" el cual tiene como parámetros " self", "start",
def djistra (self, start): #self : significa que este método pertenece a la clase y que puede acceder y manipular los atributos de la instancia actual #start: es el vértice desde el cual se calculan las distancias mínimas a todos los demás vértices en el grafo.
Cómo siguiente paso se inicializa un diccionario para almacenar las distancias mínimas desde el vértice de inicio hasta todos los demás vértices, todas las distancias deben ser infinitas a excepción de la distancia al mismo vértice start
distances = {vertex: float('infinity') for vertex in self.graph}
distances[start] = 0
Después creamos el vector donde almacenamos las distancias mínimas en este caso una cola de prioridad tipo tupla con la distancia actual y el vértice actual, no olvide el "import heapq"
import heapq queue = [(0, start)]
Posteriormente se crea un bucle mientras existan elementos en la cola
# Comienza el bucle principal mientras haya elementos en la cola de prioridad.
while queue:
# Extrae el vértice con la distancia mínima actual desde el vértice de inicio.
current_distance, current_vertex = heapq.heappop(queue)
# Comprueba si la distancia actual extraída es mayor que la distancia almacenada en el diccionario de distancias.
# Si es mayor, esto significa que hemos encontrado una distancia más corta a este vértice en un paso anterior, por lo que lo ignoramos.
if current_distance > distances[current_vertex]:
continue
# Explora los vértices adyacentes al vértice actual.
for neighbor, weight in self.graph[current_vertex].items():
# Calcula la distancia acumulada hasta el vecino desde el vértice de inicio.
distance = current_distance + weight
# Si la distancia acumulada es menor que la distancia almacenada en el diccionario de distancias para este vecino,
# actualiza la distancia almacenada y agrega el vecino a la cola de prioridad para explorar sus vecinos.
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor))
Finalmente se retorna el diccionario de distancias mínimas desde el vértice de inicio hasta todos los demás vértices
return distances
Ejemplo de implementación y uso.
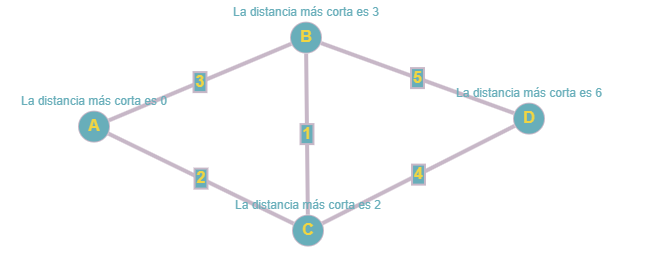
Creamos un grafo y buscamos sus distancias mas cortas:
#Creamos el Grafo
g = Graph() # Agregar vértices g.add_vertex('A') g.add_vertex('B') g.add_vertex('C') g.add_vertex('D') # Agregar conexiones g.add_edge('A', 'B', 3) g.add_edge('A', 'C', 2) g.add_edge('B', 'C', 1) g.add_edge('B', 'D', 5) g.add_edge('C', 'D', 4) # Ejecutar algoritmo de Dijkstra start_vertex = 'A' distances = g.dijkstra(start_vertex) # Mostrar resultados print("Distancias mínimas desde el vértice", start_vertex + ":") for vertex, distance in distances.items(): print("Distancia al vértice", vertex + ":", distance)
El resultado final es:
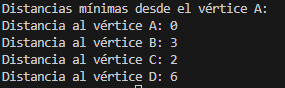
Algoritmo de Dijkstra en Python