¿Qué es el algoritmo Dijkstra?
También conocido como el camino de los caminos mínimos, su principal función es encontrar el camino mas corto en un grafo dado un vértice inicial al resto de los vértices del grafo.
El proceso que sigue es sencillo; partiendo del "Vértice Origen" se explora iterativamente los vértices adyacentes, actualizando la distancia más corta conocida desde el origen a cada vértice. En cada iteración, elige el vértice no visitado más cercano al origen y actualiza las distancias a través de él. Este proceso continúa hasta que se hayan visitado todos los vértices alcanzables desde el origen o hasta que se alcance un destino específico, si se está buscando una ruta particular.
Ejemplo practico de aplicación
Sabemos que es difícil apreciar a simple vista lo que realiza el algoritmo, pero esperemos con el siguiente ejemplo sea apreciable mas fácilmente:
Supongamos que usted es un pirata y esta en busca de un tesoro, para ello cuenta con un mapa el cual clasifica el nivel de amenaza y riesgo que tiene visitar cada lugar.
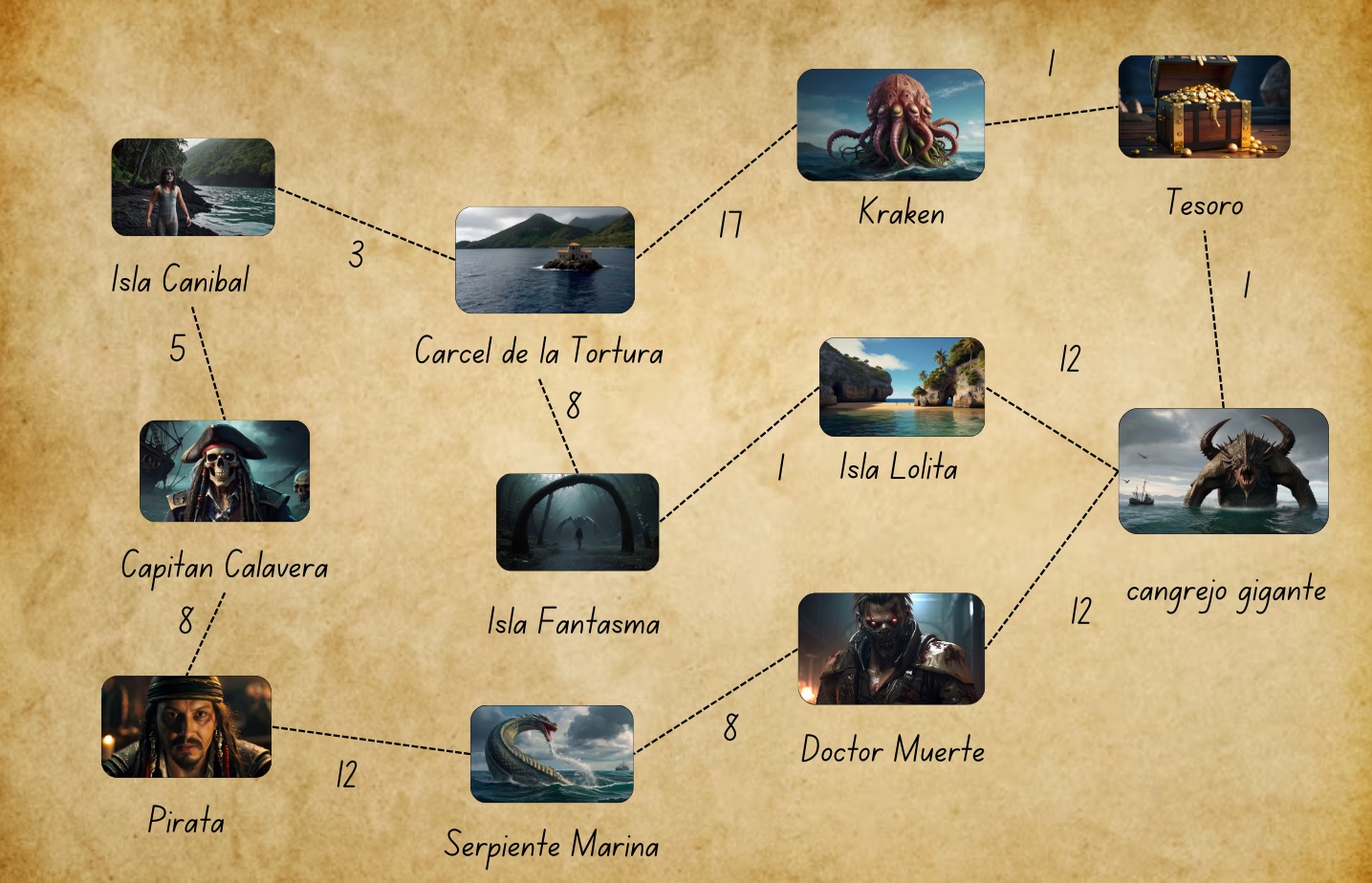
Supongamos que lo que deseara es encontrar el camino menos peligro al tesoro, lo primero que tendría que hacer es crear un grafo, donde las distancias de los vértices serán los niveles de amenaza de cada zona.
Ahora para aplicar el algoritmo Dijkstra debe hacer 3 cosas:
1) Necesitara un vector donde almacenar cada distancia mínima del vértice inicial a los demás vectores del grafo así como indicar cuando ya encontró dicha distancia mínima. El algoritmo termina cunado se encuentre la distancia mínima al vértice deseado o encuentre todas las distancias mínimas .
2) Siempre debe suponer que la distancia mínima a usted es 0 y de los demás lugares infinita "Esto porque de principio no conoce dichas distancias".
3) Es necesario contar con una variable distancia acumulada "D_a",para llevar un seguimiento de la distancia acumulada durante el proceso de exploración de los vértices. Esta distancia acumulada se calcula sumando la distancia mínima anterior (D_a) a la distancia de la arista actual (d). La distancia acumulada siempre representa la última distancia mínima seleccionada del vector de distancias.
Algoritmo:
Inicialmente usted tienen su grafo y respectivo vector de la siguiente forma.
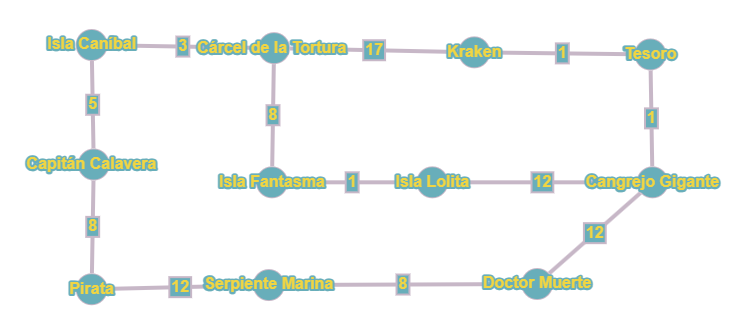
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| True | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Paso 1. Primer camino mas corto
Partiendo del pirata, el único camino mas corto es el Capitán Calavera con distancia 8, ya que por lógica es imposible que tomando el camino de 12 logremos mejorar esta marca, por ende D_a=D_a+8 y nuestro vector queda:
Vector
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| True | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Paso2. Encontrar el segundo camino mas corto.
Nos posicionamos en el vértice del Capitán Calavera, y inspeccionamos su vecinos, su único vecino es la Isla caníbal, por lo tanto la distancia acumulada es D_a=D_a+5=13, comparamos con el vector y seleccionamos la distancia mas corta no marcada como verdadero, la cual es la de la serpiente, actualizamos nuestro vector y la nueva distancia acumulada remplaza por la distancia mas corta seleccionada D_a=12.
Vector
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| True | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Paso 3.
Nos posicionamos en el vértice Serpiente marina, y inspeccionamos su vecinos, su único vecino es la Doctor Muerte, por lo tanto la distancia acumulada es D_a=D_a+8=20, comparamos con el vector y seleccionamos la distancia mas corta de las que no se a marcado como verdadero, la cual es Isla Caníbal, actualizamos nuestro vector y la nueva distancia acumulada es D_a=13.
Vector
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| True | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Paso 4.
Similar a los pasos anteriores, se realiza el proceso hasta encontrar la ruta mas corta al tesoro, con las siguientes observaciones.
1) En caso de tener 2 distancias iguales en el vector se selecciona solo 1.
2) No se puede seleccionar distancias mínimas ya marcadas.
Vector
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | ∞ | ∞ | ∞ | ∞ | ∞ |
| True | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
Paso 5.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | ∞ | ∞ | 33 | ∞ |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Paso 6.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | ∞ | 32 | 33 | ∞ |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Paso 7.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | 25 | 32 | 33 | ∞ |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Paso 8.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | 25 | 32 37 | 33 | ∞ |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Paso 9.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | 25 | 32 | 33 | 33 |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
Paso 10.
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | 25 | 32 | 33 | 33 34 |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Encontrar el camino de la distancia mínima.
Grafo
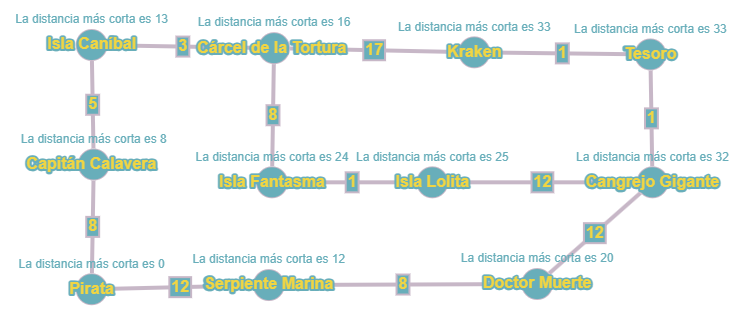
Vector
| Vértice | Pirata | Serpiente | Calavera | Caníbal | Doctor | Cárcel | Isla_Fan | Isla Lolita | Cangrejo | Kraken | Tesoro |
| distancia | 0 | 12 | 8 | 13 | 20 | 16 | 24 | 25 | 32 | 33 | 33 |
| True | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Para encontrar el camino a seguir se siguen los siguientes pasos:
1) Iniciamos con la distancia mínima al tesoro, que es 33.
2) Calculamos las distancias desde el tesoro a sus vértices adyacentes:
Distancia a Kraken = 1
Distancia a Cangrejo Gigante = 1
3)Restamos estas distancias de la distancia mínima al tesoro:
Para Kraken: 33 - 1 = 32
Para Cangrejo Gigante: 33 - 1 = 32
4)Comparamos estas diferencias con las distancias mínimas de los vértices adyacentes:
Para Kraken: 33 > 32
Para Cangrejo Gigante: 32 = 32
5)Seleccionamos el vértice que cumpla con el criterio de las distancias iguales este caso Cangrejo Gigante, encaso de que no solo una cumpla se selecciona solo un vértice.
6)Repitiendo este proceso tenemos que el camino es:
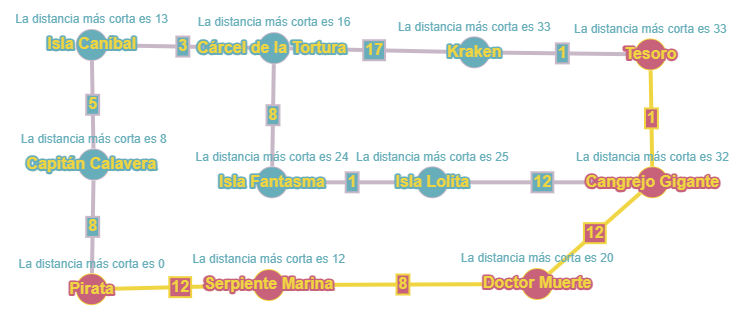
Algoritmo Dijkstra