¿Que es el algoritmo DFS y BFS ?

Ambos son algoritmos de búsqueda en grafos; la diferencia entre ambos radica principalmente en el método o pasos que siguen para recorrer en su totalidad el grafo.

DFS (Depth-First Search - Búsqueda en Profundidad).

En este método se busca como su nombre lo indica recorrer el grafo en lo profundo, los pasos que se siguen en este método son los siguientes: 

1. Partiendo de un nodo inicial se marca este como visitado, y se secciona cualquiera de los otros nodos adyacentes no visitados.
2. Una vez en el nuevo nodo se selecciona cualquiera de los nuevos nodos adyacentes no visitados y se maraca el nodo como visitado.
3. Se sigue este procedimiento hasta no tener mas nodos adyacentes o nodos no visitados.
4. Posteriormente se selecciona  el ultimo nodo no visitado registrado para continuar con el procedimiento hasta recorrer en su totalidad el grafo.

Para registra el ultimo nodos vecinos no visitados se usa generalmente una stack (pila) ya sea implementada por el programado o una stack generada por recursión, si tienes dudas sobre la recursión o que es una stack te recomendamos leer los siguientes blogs ¿Que es una Pila (Stack)?

BFS (Breadth-First Search - Búsqueda en Anchura).

Este algoritmo recorre el grafo a lo ancho, se siguen los siguientes pasos:

1. Se selecciona un nodo inicial se marca como visitado, y posteriormente se  visitan  todos sus nodos adyacentes no visitados.  
2. Cuando no queden mas nodos adyacentes no visitados de nuestro nodo inicial, se continua con los nodos adyacentes del nodos adyacentes de nutro nodo inicial.
3. Se repite este proceso hasta visitar todos los nodos del grafo.

Para saber el orden en que debemos visitar los nodos en este algoritmo generalmente se hace uso de una cola  en el que se agregan los nodos por orden en que se encontraron.

Ejemplo de ambos algoritmos. 

Sabemos que es un poco difícil comprender estos algoritmos sin un ejemplo, por ello a manera de que quede mas claro te mostramos el siguiente grafo y te mostramos paso a paso como seria el recorrido por cada método. 

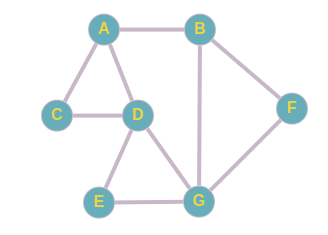
Algoritmo DFS (Profundidad):

Partimos de A lo marcamos como visitado lo agregamos a la pila y elegimos cualquiera de sus nodos vecinos, en este caso decidimos empezar  por orden alfabético y encojemos a B. 

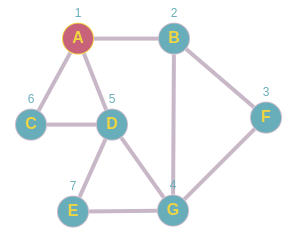
Pila: A

Una vez en B lo marcamos como visitado, y lo agregamos a la pila, ahora por orden encojemos a F.

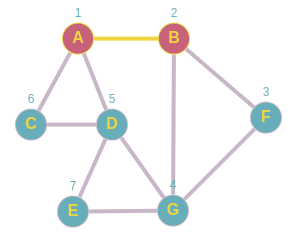
Pila: A,B,

Marcamos a F como visitado y lo agregamos a la pila, ahora encojemos a  G.  

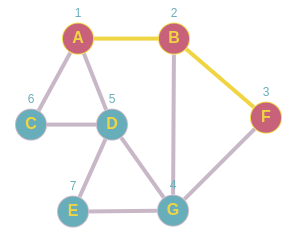
Pila: A,B,F

Nos dirigimos a  G lo marcamos como visitado lo agregamos a la pila y por orden tocaría D.

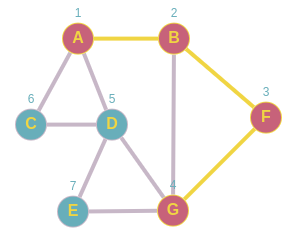
Pila A,B,F,G

Nuevamente para D lo marcamos como visitado lo agregamos a la pila y solo nos quedaría C. 

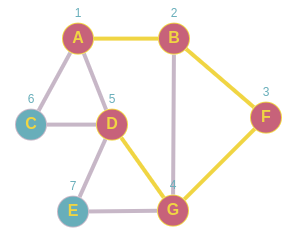
Pila A,B,F,G,D

En el nodo C los marcamos como visitado y   termina nutro recorrido pues  ya no ahí mas nodos vecinos no visitados;  por ende ahora tocaría retirar elemento de la pila el primero en salir seria D. 

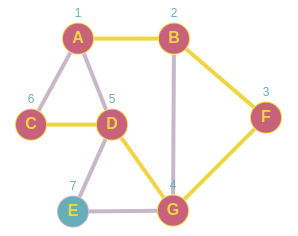
Pila A,B,F,G

Nuevamente en D el único vecino si visitar seria E, lo agregamos a la pila lo marcamos como visitado 

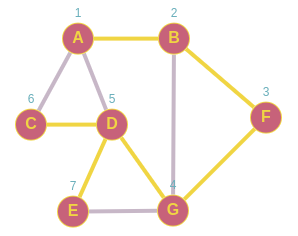
Pila A,B,F,G,E.

En E sus vecinos tanto D como G ya fueron visitados por ende tocaría sacar elementos de la pila hasta encontrar vecinos no visitados pero como  ya se recorrió todo el grafo la pila quedara finalmente vacía y termina el algoritmo. 

Algoritmo BFS (Anchura):

Partimos del nodo inicia A y  lo marcamos como visitado,  y lo agregamos a la cola, en este algoritmo es necesario evitar repetir elementos en la cola, para ello se hace uso de dos dos atributos en los nodos de los grafos Procesado y Visitado.    

Queue: A

Desencolamos a A y marcamos sus nodos adyacentes como procesados y los agregamos a la cola, paro nuestro caso los agregaremos por orden alfabético,

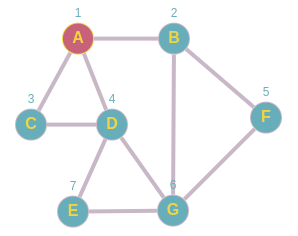
Queue: B,C,D

Ahora desencolamos y el primero en salir en B, nos dirigimos a B  marcamos como visitado y marcamos como procesados  a su vecinos F y G y los encolamos.

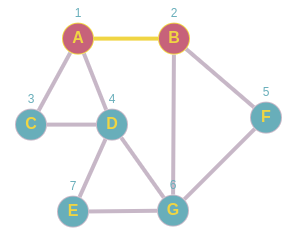
Queue: C,D,F,G

Desencolamos nuevamente obteniendo C, sin embargo al tener a sus vecinos A y D como procesados no agregamos nada a la cola.

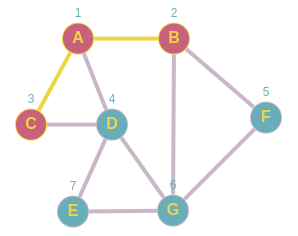
Queue: D, F, G      

El siguiente elemento en la cola es D, marcamos como visitado,  y a su vecino E lo marcamos como procesado y lo encolamos.

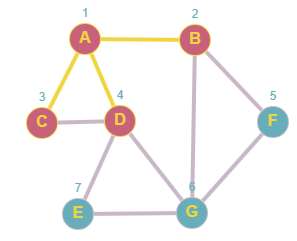
Queue: F,G,E

El elemento obtenido de la cola ahora es F, pero como sus vecinos B y G ya fueron procesados no agregamos nada.

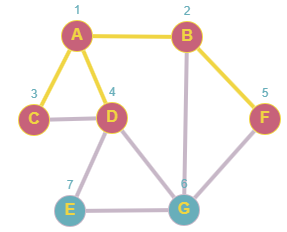
Queue: G,E.

Ahora G es el siguiente pero nuevamente no tiene ningún vecino no visitado.

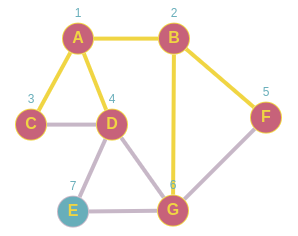
Queue: E

Finalmente E, tiene D y G que ya fueron visitados por ende el algoritmo a terminado. 

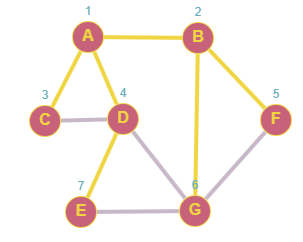
Queue: NULL