¿Qué es el algoritmo de Counting Sort ?

A diferencia de los demás algoritmos de ordenamiento como merge sort, por inserción o bubble sort, este algoritmo realiza el ordenamiento sin necesidad de  comparar los  elementos  entre si.  El algoritmo es relativamente eficiente cuando  el rango de los elementos en la lista de entrada es relativamente pequeño en comparación con el número total de elementos.  

Tiene una complejidad de tiempo lineal, lo que lo hace especialmente útil en situaciones donde se requiere una rápida clasificación de elementos dentro de un rango limitado.

Procedimiento del algoritmo 

La idea principal detrás del Counting Sort es contar el número de ocurrencias de cada elemento en la lista de entrada y utilizar esta información para construir una lista ordenada.

Los pasos básicos del algoritmo Counting Sort son los siguientes:

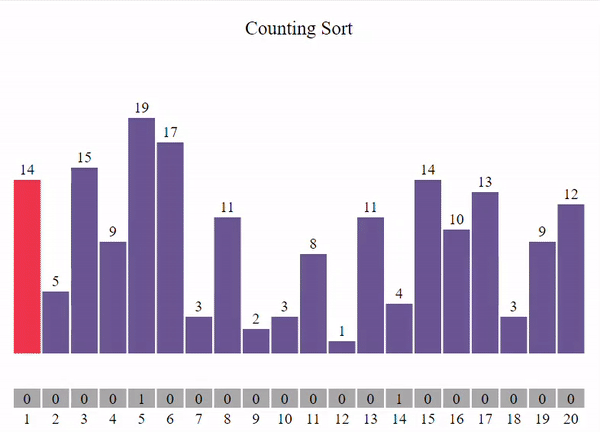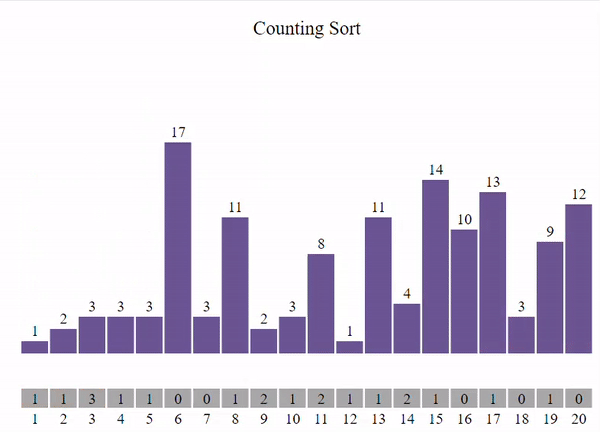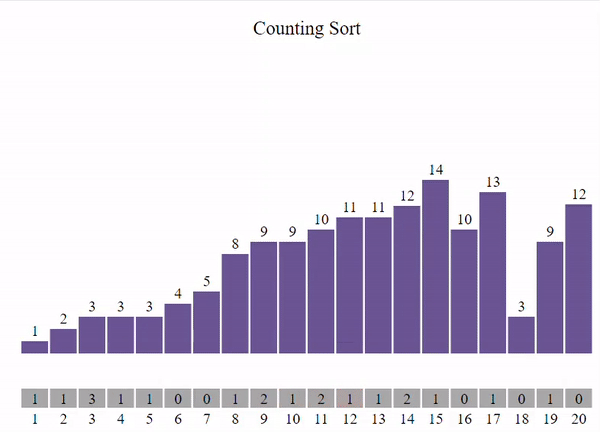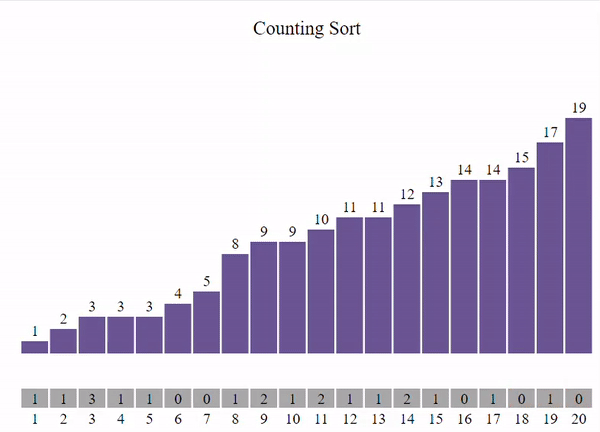
1. Conteo de ocurrencias: Escanear la lista de entrada una vez para contar cuántas veces aparece cada elemento. Esto se hace típicamente mediante el uso de un arreglo de conteo, donde el índice del arreglo representa el valor del elemento y el valor almacenado en ese índice representa el número de ocurrencias del elemento.

2. Calculando posiciones finales: Calcular las posiciones finales de cada elemento en la lista ordenada sumando las frecuencias acumuladas de los elementos anteriores. Esto asegura que los elementos con el mismo valor se ordenen correctamente.

3. Construcción de la lista ordenada: Escanear la lista de entrada nuevamente y colocar cada elemento en su posición correcta en la lista ordenada según su frecuencia y posición final calculada.

Implementación en Python.

Imagine que desea ordenar la siguiente lista 

     [14, 5, 15, 9, 19, 17, 3, 11, 2, 3, 8 ,1, 11, 4, 14, 10, 13, 3, 9, 12]

El procedimiento seria el siguiente:

La codificación  en Python:

def counting_sort(arr):

    # Encontrar el valor máximo en la lista
    max_val = max(arr)

    # Crear un arreglo de conteo con tamaño igual al valor máximo + 1
    count = [0] * (max_val + 1)
   
    # Contar las ocurrencias de cada elemento en la lista
    for num in arr:
        count[num] += 1

    # Construir la lista ordenada a partir del arreglo de conteo
    sorted_arr = []

    for i in range(len(count)):
        sorted_arr.extend([i] * count[i])
 
    return sorted_arr


# Ejemplo de uso
arr = [14, 5, 15, 9, 19, 17, 3, 11, 2, 3, 8 ,1, 11, 4, 14, 10, 13, 3, 9, 12]
print("Lista desordenada:", arr)
sorted_arr = counting_sort(arr)
print("Lista ordenada:", sorted_arr)

Resultado:

   Lista desordenada: [14, 5, 15, 9, 19, 17, 3, 11, 2, 3, 8, 1, 11, 4, 14, 10, 13, 3, 9, 12]
   Lista ordenada: [1, 2, 3, 3, 3, 4, 5, 8, 9, 9, 10, 11, 11, 12, 13, 14, 14, 15, 17, 19]      

Ventajas y Desventajas. 

Ventajas:

1. Eficiencia en tiempo lineal: Counting Sort tiene una complejidad de tiempo lineal O(n + k), donde "n" es el número de elementos en la lista y "k" es el rango de valores en la lista. Esto hace que Counting Sort sea altamente eficiente para listas grandes, especialmente cuando el rango de valores es relativamente pequeño.

2. Estabilidad: Counting Sort es un algoritmo estable, lo que significa que conserva el orden relativo de los elementos con claves iguales. Esto es importante en aplicaciones donde se requiere mantener el orden relativo original de los elementos.

3. No requiere comparaciones entre elementos: A diferencia de otros algoritmos de ordenamiento, como QuickSort o MergeSort, Counting Sort no requiere comparaciones directas entre los elementos. En su lugar, utiliza la información sobre las frecuencias de los elementos para construir la lista ordenada.

4. Adaptable para rangos pequeños de valores: Counting Sort es particularmente eficiente cuando el rango de valores en la lista es pequeño en comparación con el número de elementos. En tales casos, el espacio adicional requerido para el arreglo de conteo es justificado por la mejora en la complejidad temporal.

Desventajas:

1. Requiere espacio adicional: Counting Sort requiere un arreglo de tamaño igual al rango de valores en la lista, lo que puede consumir una cantidad significativa de memoria, especialmente cuando el rango de valores es grande. Esto puede ser una limitación en sistemas con recursos limitados.

2. No adecuado para rangos grandes de valores: Counting Sort puede volverse ineficiente cuando el rango de valores en la lista es muy grande en comparación con el número de elementos, ya que el tamaño del arreglo de conteo será proporcional al rango de valores.

3. No es adecuado para datos no enteros: Counting Sort es específico para datos enteros y no es adecuado para otros tipos de datos, como cadenas de texto o datos de punto flotante.