¿Qué es el algoritmo de la baraja?
También conocido como algoritmo de "Inserción directa", es un método de ordenamiento sencillo e intuitivo que
funciona recorriendo una lista de elementos y colocando cada elemento en su posición correcta dentro de la lista ordenada. Se le dar el nombre de baraja debido a su similitud con el proceso de
ordenar un mazo de cartas numeradas en forma arbitraria; normalmente se requiere 


Procedimiento del algoritmo.
El algoritmo se consta de la siguiente lista de pasos.
1. Inicio: El proceso comienza con una lista de elementos desordenados.
2.Recorrer la lista: Se recorre la lista de izquierda a derecha, comenzando desde el segundo elemento (índice 1) hasta el último elemento (índice n-1), donde "n" es el número total de elementos en la lista.
3.Seleccionar un elemento: En cada iteración del recorrido, se selecciona el elemento actual que se desea insertar en la posición correcta dentro de la lista ordenada.
4.Comparar y desplazar: Se compara el elemento seleccionado con los elementos que están antes en la lista ordenada. Se recorren los elementos hacia la derecha mientras el elemento seleccionado sea menor que el elemento actual en la posición de comparación.
5. Insertar el elemento: Una vez que se encuentra la posición correcta para el elemento seleccionado, se inserta en esa posición, desplazando los elementos si es necesario para hacer espacio.
6. Repetir: Se repiten los pasos 3 a 5 para cada elemento de la lista, avanzando de izquierda a derecha.
7. Fin: Una vez que todos los elementos han sido insertados en su posición correcta, la lista estará completamente ordenada.
Ejemplo de Implementación en Python.
Imagine que se desea ordenar la lisita de elementos:
6 5 3 1 8 7 2 4
El proceso que se tendría que seguir es el siguiente:
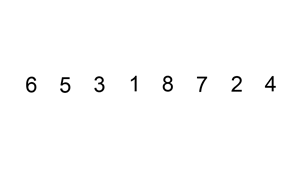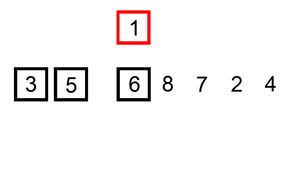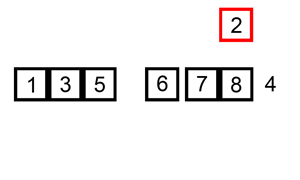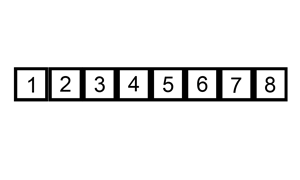
Animación obtenida de Wikipedia: https://es.wikipedia.org/wiki/Ordenamiento_por_inserci%C3%B3n
La codificación del algoritmo en Python seria el siguiente:
def insertion_sort(arr):
# Comenzamos recorriendo la lista desde el segundo elemento
for i in range(1, len(arr)):
# Guardamos el valor del elemento actual que vamos a insertar en la lista ordenada
current_value = arr[i]
# Guardamos la posición del elemento actual
position = i
# Comparamos el elemento actual con los elementos antes de él en la lista ordenada
# y desplazamos los elementos hacia la derecha mientras el valor actual sea menor
# que el elemento en la posición de comparación
while position > 0 and arr[position - 1] > current_value:
arr[position] = arr[position - 1]
position -= 1
# Insertamos el valor actual en la posición correcta dentro de la lista ordenada
arr[position] = current_value
# Ejemplo de uso del algoritmo de ordenamiento por inserción
arr = [5, 2, 4, 6, 1, 3]
print("Lista desordenada:", arr)
insertion_sort(arr)
print("Lista ordenada:", arr)
El resultado obtenido es el siguiente:
Lista desordenada: [5, 2, 4, 6, 1, 3]
Lista ordenada: [1, 2, 3, 4, 5, 6]
Ventajas y desventajas del algoritmo
- Ventajas:
1) Simple implementación: Es fácil de entender e implementar, lo que lo hace ideal para propósitos educativos y para aquellos que están aprendiendo sobre algoritmos de ordenamiento.
2) Eficiente para pequeñas cantidades de datos: Es muy eficiente cuando se trata de ordenar conjuntos de datos pequeños o casi ordenados. En estos casos, su complejidad de tiempo es cercana a lineal, lo que significa que puede superar a algoritmos de ordenamiento más complejos.
3) Eficiente para datos parcialmente ordenados: Si una gran parte de los elementos de la lista ya están en orden, el algoritmo de inserción tiene un rendimiento muy bueno, ya que solo necesita mover algunos elementos para ordenar la lista completa.
4) Requiere menos espacio de memoria: El algoritmo de inserción ordena los elementos dentro de la misma lista sin necesidad de utilizar memoria adicional, lo que lo hace eficiente en términos de espacio de memoria. - Desventajas:
1) Ineficiente para grandes cantidades de datos: A medida que el tamaño de los datos aumenta, la eficiencia del algoritmo de inserción disminuye considerablemente. Su complejidad de tiempo en el peor caso es cuadrática (O(n^2)), lo que significa que puede ser muy lento en comparación con otros algoritmos de ordenamiento como mergesort o quicksort para grandes conjuntos de datos.
2) Dependiente del orden inicial: El rendimiento del algoritmo puede variar dependiendo del orden inicial de los elementos en la lista. Si la lista está invertida o casi invertida, el algoritmo tomará más tiempo en ordenarla en comparación con una lista que esté más cerca de estar ordenada.
3) No es estable con respecto al orden original: A diferencia de algunos otros algoritmos de ordenamiento como mergesort, el algoritmo de inserción no es estable con respecto al orden original de los elementos. Esto significa que puede cambiar el orden relativo de los elementos con el mismo valor durante el proceso de ordenamiento.
¿Qué es el Algoritmo de la Baraja ?