¿Qué es el algoritmo de Marge Sort ?

El algoritmo de Merge Sort, es de los mas eficientes algoritmos de búsqueda y ordenamiento , que se basa en el principio "divide y conquista", es fácil de paralelizar e implementar recursivamente, también es conocido como ordenamiento por mezcla, su complejidad es  O(n log n).  Fue desarrollado  en  1945 por John Von Neumann. 

Procedimiento.

A grandes rasgos el proceso por el que organiza los elementos es el siguiente: 

1. Divide: La lista no ordenada se divide en dos sublistas de aproximadamente la misma longitud. Este proceso se repite recursivamente hasta que cada sublista tenga un solo elemento, lo que indica que está ordenada.

2. Conquista: Durante el proceso de división, las sublistas se fusionan de manera ordenada. Esto implica comparar los elementos de las sublistas y colocarlos en orden en una nueva sublista temporal.

3. Combina: En esta etapa, las sublistas se fusionan gradualmente para formar sublistas más grandes y ordenadas. Este proceso se repite hasta que se haya completado la fusión de todas las sublistas en una única lista ordenada.

Implementación en Python  

Imaginemos que deseamos organizar la siguiente lista: 

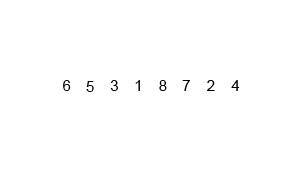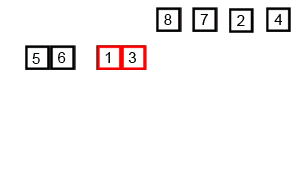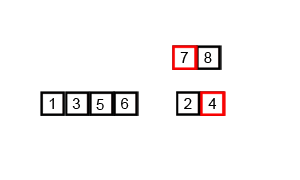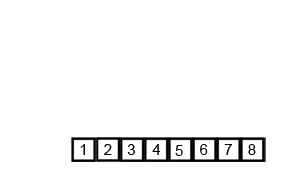
                                Imagen Obtenida de Wikipedia:                 https://es.wikipedia.org/wiki/Ordenamiento_por_mezcla  

El procedimiento seria el siguiente.

Su codificación en Python :

def merge_sort(arr):

    # Verificamos si la lista tiene más de un elemento
    if len(arr) > 1:
        # Calculamos el punto medio de la lista
        mid = len(arr) // 2

        # Dividimos la lista en dos sublistas
        left_half = arr[:mid]
        right_half = arr[mid:]

        # Llamada recursiva para ordenar la primera mitad
        merge_sort(left_half)
        
        # Llamada recursiva para ordenar la segunda mitad
        merge_sort(right_half)
        
        # Índices para recorrer las sublistas
        i = j = k = 0

        # Combinamos las sublistas ordenadas en una sola lista ordenada
        while i < len(left_half) and j < len(right_half):

            if left_half[i] < right_half[j]:
                arr[k] = left_half[i]
                i += 1

            else:
                arr[k] = right_half[j]
                j += 1
            k += 1

        # Verificamos si quedan elementos en la primera sublista
        while i < len(left_half):
            arr[k] = left_half[i]
            i += 1
            k += 1
        
        # Verificamos si quedan elementos en la segunda sublista
        while j < len(right_half):
            arr[k] = right_half[j]
            j += 1
            k += 1


# Ejemplo de uso del algoritmo Merge Sort
arr = [6, 5, 3, 1, 8, 7, 2, 4]
print("Lista desordenada:", arr)
merge_sort(arr)
print("Lista ordenada:", arr)

El resultado es el siguiente: 

  Lista desordenada: [6, 5, 3, 1, 8, 7, 2, 4]    
   Lista ordenada: [1, 2, 3, 4, 5, 6, 7, 8]         

Ventajas y Desventajas. 

• Ventajas:

1. Eficiencia en todo tipo de casos: El algoritmo Merge Sort tiene una complejidad de tiempo de O(n log n) en todos los casos, lo que lo hace muy eficiente incluso para conjuntos de datos grandes y desordenados. Esta eficiencia lo hace especialmente útil en aplicaciones donde se necesita ordenar grandes cantidades de datos.

2. Estabilidad: Merge Sort es un algoritmo estable, lo que significa que conserva el orden relativo de los elementos con claves iguales. Esto lo hace útil en situaciones donde la estabilidad del ordenamiento es importante.

3. Implementación sencilla y comprensible: La lógica detrás del algoritmo Merge Sort es relativamente simple de entender, ya que se basa en el concepto de "dividir y conquistar". Esto facilita su implementación y depuración, lo que lo hace adecuado para enseñar y aprender sobre algoritmos de ordenamiento.

4. No requiere memoria adicional: Aunque Merge Sort requiere dividir la lista original en sublistas, no necesita memoria adicional para almacenar los elementos mientras se están ordenando. Esto lo hace eficiente en términos de uso de memoria.

• Desventajas:

1. Requiere más memoria auxiliar: A pesar de no necesitar memoria adicional para almacenar los elementos, Merge Sort requiere memoria auxiliar para almacenar las sublistas temporales durante el proceso de combinación. Esta necesidad de memoria adicional puede ser una desventaja en sistemas con restricciones de memoria.

2. No es óptimo para listas pequeñas: Aunque Merge Sort es muy eficiente para grandes conjuntos de datos, su desempeño puede ser peor que otros algoritmos de ordenamiento, como el algoritmo de inserción, para listas pequeñas o casi ordenadas. Esto se debe al costo adicional de dividir y combinar las sublistas.

3. Implementación recursiva: Aunque la recursión es una característica poderosa y elegante de Merge Sort, puede causar problemas de rendimiento y límites de profundidad de recursión en sistemas con recursos limitados o con grandes conjuntos de datos.