¿Qué es el algoritmo QuickSort?
El algoritmo QuickSort, creado por Tony Hoare en 1959, es un eficiente y ampliamente utilizado algoritmo de ordenamiento que se basa en el principio de dividir y conquistar. A diferencia de MergeSort, que divide el arreglo en mitades iguales, QuickSort utiliza un pivote para dividir el arreglo en subarreglos.
El proceso comienza eligiendo un elemento como pivote y reordenando el arreglo de manera que todos los elementos menores que el pivote estén a su izquierda y todos los elementos mayores estén a su derecha. Luego, el algoritmo se aplica recursivamente a cada subarreglo generado.
El rendimiento del QuickSort depende en gran medida de la elección del pivote, pero en promedio tiene una complejidad de O(n log n). Sin embargo, en el peor de los casos, cuando el pivote siempre es el mínimo o el máximo, la complejidad puede degenerar a O(n^2). A pesar de esto, QuickSort sigue siendo ampliamente utilizado debido a su eficiencia y simplicidad de implementación.
Diferencias con MergeSort.
- QuickSort:
1. Divide el arreglo utilizando un pivote.
2. No tiene una etapa de combinación explícita.
3. No es estable en su implementación básica.
4. Puede degradarse a O(n^2) en el peor caso.
5. Puede ser implementado "in-place". - MergeSort:
1. Divide el arreglo en mitades iguales.
2. Tiene una etapa de combinación donde las sublistas se fusionan.
3. Es estable.
4. Siempre tiene complejidad O(n log n).
5. Tiende a usar más memoria.
Pasos del algoritmo.
Elección del pivote: Selecciona un elemento del arreglo como pivote. Este elemento puede ser elegido de diversas maneras, como el primer elemento, el último elemento o un elemento al azar.
Partición: Reordena los elementos del arreglo de manera que todos los elementos menores que el pivote estén a su izquierda y todos los elementos mayores estén a su derecha. Esto se hace de tal manera que el pivote quede en su posición final en el arreglo ordenado. Este paso también divide el arreglo en dos subarreglos alrededor del pivote.
Recursión: Aplica recursivamente los pasos 1 y 2 a los subarreglos generados por la partición. Es decir, se repite el proceso de selección de pivote y partición en cada subarreglo hasta que el arreglo esté completamente ordenado. Este paso utiliza la naturaleza del paradigma "dividir y conquistar".
Combinación (implícita): No hay una etapa de combinación explícita en QuickSort, ya que los elementos se van ordenando "in-place" durante el proceso de partición.
Implementación en Python.
Imagine que desea ordenar la siguiente lista de elementos:
[ 6, 5 ,3 ,1 ,8 ,7 ,2 ,4 ]
El proceso seria el siguiente:
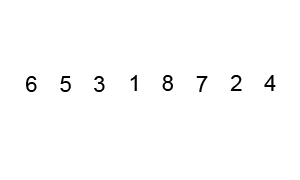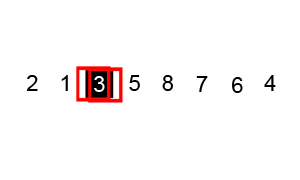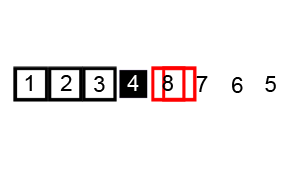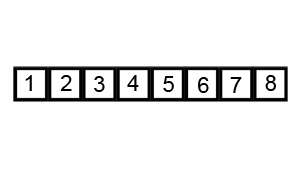
Imagen, Matt Chan.
El código en Python seria el siguiente:
def quicksort(arr):
# Llamada inicial al helper que implementa QuickSort
_quicksort(arr, 0, len(arr) - 1)
def _quicksort(arr, low, high):
# Función helper que implementa QuickSort recursivamente
if low < high:
# Encuentra el índice del pivote (el elemento que estará en su posición final)
pivot_index = partition(arr, low, high)
# Llama recursivamente a quicksort para las sub-listas a la izquierda y a la derecha del pivote
_quicksort(arr, low, pivot_index - 1)
_quicksort(arr, pivot_index + 1, high)
def partition(arr, low, high):
# Función para particionar el arreglo alrededor de un pivote
# Selecciona el pivote (en este caso, el último elemento del rango)
pivot = arr[high]
# Índice del primer elemento que será mayor que el pivote
i = low
for j in range(low, high):
# Si el elemento actual es menor o igual al pivote, lo intercambia con el elemento en arr[i]
if arr[j] <= pivot:
arr[i], arr[j] = arr[j], arr[i]
i += 1
# Coloca el pivote en su posición final intercambiándolo con el elemento en arr[i]
arr[i], arr[high] = arr[high], arr[i]
# Retorna el índice del pivote
return i
# Lista de ejemplo
arr = [6, 5, 3, 1, 8, 7, 2, 4]
# Llama a la función de ordenamiento QuickSort
quicksort(arr)
# Imprime la lista ordenada
print("Lista ordenada:", arr)
Resultado:
Lista ordenada: [1, 2, 3, 4, 5, 6, 7, 8]
Ventajas y Desventajas:
Ventajas:
1. Eficiencia promedio: En promedio, QuickSort tiene un rendimiento muy bueno, con una complejidad de tiempo de O(n log n) en el caso promedio, lo que lo hace muy eficiente para ordenar grandes conjuntos de datos.
2. Eficiente en memoria: QuickSort puede ser implementado para ordenar "in-place", lo que significa que no requiere memoria adicional más allá de la que ya se está utilizando para el arreglo, haciendo que su uso de memoria sea eficiente.
3. Buena para arreglos grandes: QuickSort tiende a ser más eficiente que otros algoritmos de ordenamiento como MergeSort cuando se trata de arreglos grandes o listas enlazadas, debido a su menor requerimiento de memoria y a su rendimiento en promedio.
4. Implementación simple: La implementación del algoritmo QuickSort puede ser relativamente simple y directa, lo que lo hace fácil de entender y de implementar en diversos lenguajes de programación.
Desventajas:
1. Sensibilidad al pivote: La eficiencia del QuickSort depende en gran medida de la elección del pivote. Si el pivote se elige mal, especialmente en casos extremos como cuando el arreglo ya está ordenado o está casi ordenado, la eficiencia del algoritmo puede degradarse significativamente, incluso hasta O(n^2).
2. Inestabilidad: QuickSort no es estable en su implementación básica, lo que significa que no necesariamente conserva el orden relativo de elementos con claves iguales. Sin embargo, esto puede ser abordado con algunas técnicas adicionales en la implementación.
3. Peor caso de complejidad: Aunque en promedio QuickSort tiene una complejidad de O(n log n), en el peor caso puede degenerar a O(n^2), lo que lo hace menos deseable en situaciones donde se requiere garantizar tiempos de ejecución consistentemente buenos.
4. No apto para datos sensibles al orden: QuickSort puede ser ineficiente para arreglos donde los datos están cerca de su posición ordenada final, ya que su rendimiento está relacionado con la partición equitativa del arreglo.