Árbol Binario de Búsqueda.

También conocido como BST ( Binary Search Tree ), es una  de las aplicación de un árbol binario, de forma que para todos los  elemento, los elementos mayores a ´el, se ubican en su rama derecha, mientras que los elementos menores van en su rama izquierda.  

Propiedades de un árbol binario de búsqueda.

Al ser a fin de cuentas un  árbol binario de búsqueda es un caso particular de un árbol binario, por lo que heredad alguna de sus propiedades y agrega algunas otras   es decir   

1. Cada nodo tiene como máximo dos hijos.
2. El hijo izquierdo de un nodo tiene un valor menor que el valor del nodo padre.
3. El hijo derecho de un nodo tiene un valor mayor que el valor del nodo padre.
   

Elementos en un árbol binario de Búsqueda

A continuación se explican los elementos principales del árbol de búsqueda:

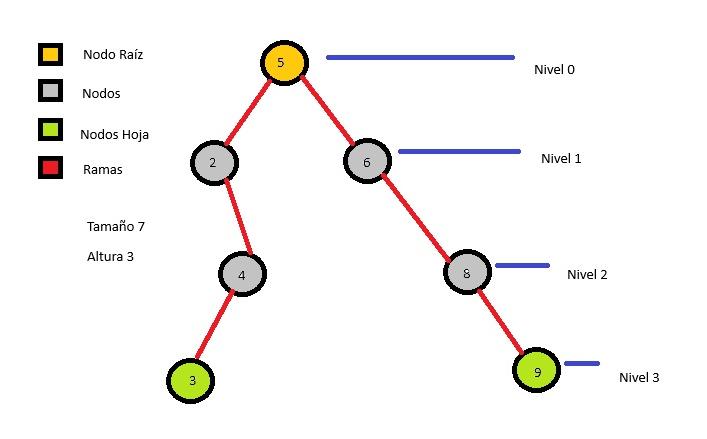
• Nodos: Elementos básicos del árbol que almacena la información, todos los nodos tienen padre a excepción de la raíz   
• Nodo Raiz.: Este nodo no tiene padre es donde, es el nodo donde parten todas la ramas 
  
• Hojas o nodos:  Son nodos que no tienen ningún hijo se encuentran en los niveles mas bajos del  árbol. 

• Ramas:  Son las conexiones entre los nodos y forman al árbol. 

• Nodo padre: Es aquel que tiene uno a mas nodos hijos 

• Nodos hijos: Es el elemento que tiene un elementos donde procede es decir un nodo padre, cada nodos hijo pude tener a su vez uno o mas nodos hijos. 

• Profundidad:   Es el nivel de un nodo dentro del árbol, contando desde la raíz hasta el nodo en cuestión. La profundidad de la raíz es 0, y la profundidad aumenta a medida que se desciende en el árbol.

• Altura: Es la longitud del camino más largo desde un nodo hasta una hoja. En otras palabras, es la distancia máxima entre la raíz y cualquier hoja del árbol. La altura de un árbol vacío es -1, y la altura de un árbol con un solo nodo (la raíz) es 0. La altura h en el peor de los casos es siempre el mismo tamaño que el número de elementos disponibles. Y en el mejor de los casos viene dada por la expresión  

• Tamaño: Es el número total de nodos en el árbol,

Ejemplo de Aplicación.

Imagine que desea construir el árbol mostrado en la  ilustración anterior, el procesos seria al siguiente.  

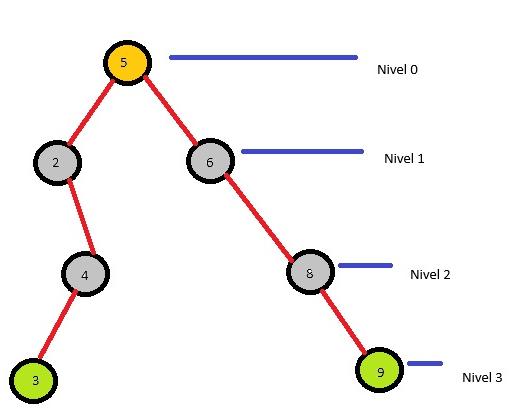
• 5 (raíz)
• 4 (hijo izquierdo de 5)
• 6 (hijo derecho de 5)
• 8 (hijo derecho de 6)
• 9 (hijo derecho de 8)
• 2 (hijo izquierdo de 4)
• 3 (hijo derecho de 2)

• Desbalanceo en arboles de Binarios de Búsqueda.

Como es posible notar el árbol no siempre asegurara tener  la misma altura del lado en los sub arboles derechos que izquierdos, a esta situación se le conoce como desbalanceo. cuando un árbol  esta desbalanceado , las operaciones de inserción, búsqueda y eliminación pueden volverse menos eficientes, ya que la propiedad fundamental de un BST de tener tiempos de operación logarítmicos puede perderse.  

El árbol balanceado seria el siguiente: 

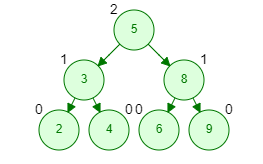
Para crear una árbol balanceado de Búsqueda se puede seguir los siguientes métodos.

• Rotación simple
• Rotación Doble Izquierda (DI).
• Rotación Doble Derecha (DD)