¿Que es un Grafo?
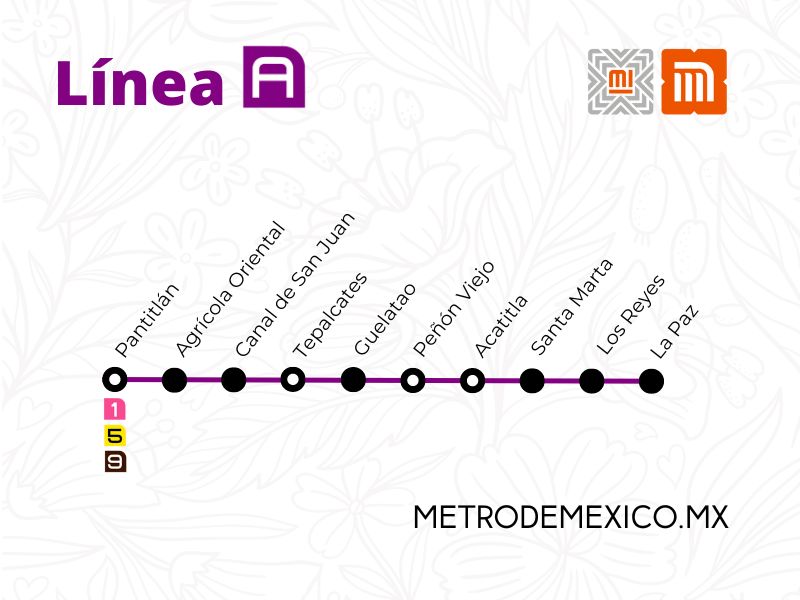
Un grafo a grandes rasgos es una estructura de datos que permite representar relaciones entre elementos; ejemplos cotidianos un grafo son un árbol genealógico, el mapa de las diversas lineas del metro de la Ciudad de México, un laberinto, las redes sociales como Facebook, Twitter o LinkedIn, en resumen cualquier cosa que se pueda representar relaciones entre elementos se pude considerar un grafo.
Elementos de un Grafo
Los grafos se componen principalmente de dos elementos vértices (nodos) y aristas (conexiones ).
Retomando el ejemplos de las lineas del metro de la ciudad de México, si quisiéramos representarlas por medio de un grafos las estaciones del metro serian los vértices o nodos y el trayecto que une a ambas estaciones serian las aristas conexiones.
Tipos de Grafos
Existen distintos tipos de grafos pero son principalmente 4.
- Ponderados. ( existe un peso en sus conexiones )
- No Ponderados. ( No existe un peso en sus conexiones )
- Dirigidos. ( Es posible ir de A a B pero no de B a A)
- No Dirigidos. (Es posible ir de A a B y de B a A)
De estos 4 tipos podemos tener múltiples combinaciones ponderados no dirigidos, no ponderados dirigidos etc.
De forma que quede mas clara se dará un ejemplo de cada tipo:
Grafo Ponderado.
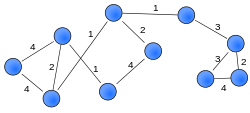
Cada conexión tiene un costo o peso, retomando el ejemplo del metro de la Ciudad de México no siempre tardamos la mismo en viajar entre una estación y otra, el tiempo entre estas estaciones representaría la ponderación (precio).
Grafo no Ponderado
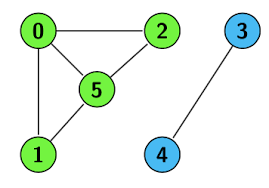
Es la contra parte del ejemplo anterior, en este tipo de grafo no existe un peso en las conexiones, si tardáramos lo mismo para viajar entre estaciones no importaría el tiempo , y por lo tanto podríamos omitir el tiempo.
Grafo Dirigido.
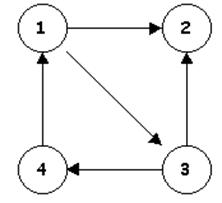
En este tipo de grafo se suele representar las direcciones de las conexiones con flechas, este tipo de grafo no cumple la siguiente propiedad para todos los caso "es posible viajar de A a B, pero no de B a A ". en el ejemplo mostrado a continuación es posible ir de 1 a 2 pero no de 2 a 1,
Grafo no dirigido
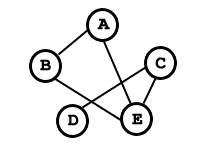
Este tipo de grafo es un grafo en donde es cada una de las conexiones vértices cumplen con la siguiente propiedad "Es posible ir de A a B y de B a A". en el siguiente ejemplo se muestra un ejemplo de este tipo de grafo.
Ahora, si eres observador notaste que para muchos de los grafos mostrados se combinan siempre dos tipos ponderado o no ponderado y dirigido o no dirigido, esto es porque normalmente es necesario definir estas dos características para representar un grafo tendrá peso o no tendrá peso, sera dirigido o no dirigido.
Programación para un grafo.
Si bien la teoría en si del grafo no es tan complicada, la dificultad radica en pasar de la idea a la computadora existir diversas formas de programar a un grafo pero las dos mas comunes son:
Matriz de Adyacencia.
En este método de programación las columnas corresponden a cada uno de los nodos o vértices del grafo y las filas a cada conexión con otros nodos, se rellena cada espacio con un 1 o 0 si existe una conexión o no
Listas enlazadas.
Para este método se utiliza una lista de listas en la que cada elemento en la lista contiene otra lista, donde se agregan los conexiones con otros elementos.
Ambos métodos tienen sus ventajas y desventajas, ahorro de espacio, velocidad para encontrar un elemento si te interesa mas sobre esto puedes visitar nutro blog donde hablamos mas a detalle /link/.
Algoritmos BFS y DFS.
Son algoritmo de búsqueda utilizados para recorrer o buscar elementos en estructuras de datos como árboles o grafos, y su principal diferencia es la forma que se técnica para recorrer el grafo ya que el BFS (Breadth-First Search) recorra el grafo a lo ancho y DFS (Depth-First Search) lo realizara a lo ancho; si te interesa mas sobre esto puedes visitar nutro blog donde hablamos mas a detalle Algoritmos DFS y BFS
¿Que es un grafo?